Vnitřní a jiné síly
Statické síly
Kohezivní síla
Na každou částici (molekulu) kapaliny působí sousední částice přitažlivými kohezními silami. Podstatu kohezních sil lze vysvětlit elektrostatickým přitahováním a odpuzováním molekul. Plný výklad podává až kvantová fyzika. Vzájemné působení je pouze krátkého dosahu a klesá mnohem rychleji než s druhou mocninou vzdálenosti. Přitažlivé působení každé částice je tak možné omezit na velmi malý kulový prostor v jehož středu se nachází uvažovaná částice. Tento prostor se nazývá sféra molekulárního působení a jeho poloměr ρ se označuje jako poloměr molekulárního působení.
Rozložíme sílu, která působí na vybranou molekulu na složku rovnoběžnou s povrchem kapaliny (horizontální) a složku, která je k povrchu kapaliny kolmá (vertikální).
Horizontální složky se při rovnoměrném rozložení molekul v kapalině vzájemně vyruší, neboť v obou polovinách sféry (pravé i levé) můžeme předpokládat přibližně shodný počet molekul. Tyto vodorovné složky samozřejmě vytvářejí určité napětí, které má u molekul na povrchu kapaliny charakter povrchového napětí.
Vertikální složky se vyruší jen pokud se sféra molekulárního působení nachází celá uvnitř kapaliny. Pokud je však vzdálenost od povrchu menší, je ve vertikálním směru rozložení částic kapaliny nesymetrické, což má za následek, že síly nebudou vyrovnány a výsledná síly bude nenulová a orientovaná do kapaliny. Se zmenšující se vzdáleností od povrchu tato síla roste a maximální hodnoty dosáhne pro molekuly, které se nachází právě na povrchu kapaliny.
 1
1
Kohezivní tlak
V důsledku působení kohezních sil je tlak na povrchu menší než uvnitř kapaliny a jeho velikost roste se vzdáleností od povrchu kapaliny, přičemž maximální hodnoty dosahuje ve vzdálenosti ρ. Tento celkový vzrůst tlaku se nazývá kohezním tlakem. Kohezní tlak nelze přímo měřit, ale lze jej pouze odhadnou na základě teoretických podkladů. Značné hodnoty kohezního tlaku (až kolem 109Pa) souvisí s nízkou stlačitelností kapalin. Není-li povrch kapaliny vodorovný, vzniká v důsledku jeho zakřivení dodatečný tzv. kapilární tlak.
Povrchové napětí a kapilární jevy (krajový úhel, kapilární elevace a deprese) lze považovat za důsledek kohezních sil.
 2
2 Povrchové napětí
Povrchové napětí je výsledkem vzájemné interakce přitažlivých sil molekul nebo atomů, z nichž se skládá povrchová vrstva. Je definováno jako síla vztažená na jednotku délky myšleného řezu povrchem kapaliny
![]()
Povrch kapaliny se chová tak, jako by byl tvořen velmi tenkou pružnou vrstvou, která se snaží při daném objemu kapaliny zaujímat co nejmenší plochu. Pokud by na kapalinu nepůsobily vnější síly, měla by kulový tvar, protože koule má ze všech těles stejného objemu nejmenší povrch. Povrchové napětí je definováno jako práce vnějších sil potřebná k zvětšení plochy vydělená hodnotou změny plochy. Je to vlastně hustota povrchové energie.
![]()
Kapka kapaliny na pevn ém povrchu může zaujmout různý tvar na základě povrchového napětí kapaliny ve styku se vzduchem danou kohezivními silami, povrchového napětí mezi kapalinou a tuhou látkou danou adhezivními silami a konečně povrchovým napětím pevné látky ve styku se vzduchem.
Také kapalina v nádobě může zaujmout u stěny různý tvar. Pro síly povrchového napětí působící na styku kapalina, pevné látky a vzduchu platí následující rovnováha:
![]()
Velikost povrchového napětí pro vodu ve styku se vzduchem σkp při 20°C je 73.10-3 N/m, pod dosazení dostáváme:
![]()
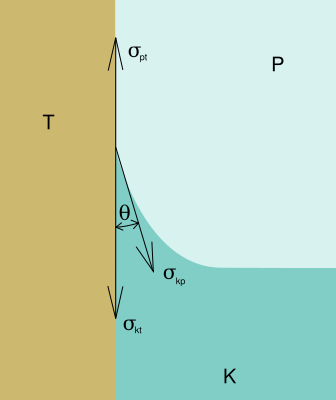
kde Θ se nazývá stykový úhel a jeho kosinus nabývá hodnoty od 1 do -1. Velikost povrchového napětí (povrchovou energií) mezi kapalnou a pevnou látkou je dána adhezivními silami.
Stykový úhel Θ je tedy úhel, který svírá okraj kapaliny s pevným povrchem. Velikost stykového úhlu je závislá na rozdílu povrchového napětí tuhého tělesa vzhledem k plynu a tuhého tělesa vzhledem ke kapalině.
Je-li stykový úhel Θ roven 0, kapalina dokonale smáčí stěnu. Je-li roven 180° kapalina stěnu dokonale nesmáčí. Podobně se (do jisté míry) chovají některé organické látky, např. alkohol.
Je-li roven 90° kapalina v kapalina vytváří přesně polokulovitou kapku, nebo v případě povrchu v trubici vytváří volný povrch.
Pro vodu ve skleněné nádobě je stykový úhel Θ roven 8°. Pro rtuť ve skleněné nádobě je stykový úhel Θ roven 128°.
 3
3
Povrchové napětí (povrchová energie) mezi kapalnou a pevnou látkou
Je dána adhezivními silami. Adhezivní síly vyjadřují schopnost dvou (především rozdílných) materiálů spolu přilnout. Jedná se o mezimolekulární přitažlivé chemické a fyzikální síly na styčných plochách v nerovnostech a pórech materiálů. Pěti základními mechanizmy adheze jsou:
- mechanická adheze (např. suchý zip),
- chemická adheze (zprostředkována chemickou kovalentní vazbou),
- disperzní adheze (Van der Waalsovy síly nekovalentní přitažlivé síly, které působí mezi nepolárními molekulami a jsou důsledkem vzniku okamžitého elektrického dipólu)
- elektrostatická adheze
- difúzní adheze (polymery).
Povrchové napětí pevné látky ve styku se vzduchem
Odhadem založeným na několika přímých experimentálních stanoveních a nukleačních studiích lze konstatovat, že pevné látky v blízkosti bodu tání mají o 10 až 20% vyšší povrchovou energii než látky v kapalném stavu - přibližně v poměru sublimačního a výparného tepla. Hodnota povrchové energie odhadnutá při teplotě tání může být pak extrapolována na jinou teplotu (viz povrchové napětí kapalin).
Některým vodním živočichům umožňuje povrchové napětí bezpečný pohyb po hladině vody (např. vodoměrky).
Co je to lotosový efekt?
Komáři a moskyti dokonce využívají povrchové napětí vody oběma způsoby. Na vodní hladině unesou až patnáctinásobek své váhy a můžou po ní skákat, protože mají konce nožiček pokryty drobnými lamelovitými lištami, které odpuzují vodu (viz obr.).
 4
4  5
5  6
6 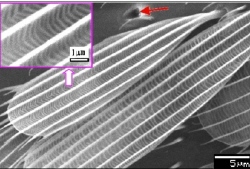 7
7
Povrchově aktivní látky snižují hodnotu povrchového napětí, jejich efekt lze popsat laterálním tlakem π, který působí proti povrchovému napětí. Mezi povrchově aktivní látky patří saponáty obsažené v pracích a čistících prostředcích. Kontaminací přírodních vod tak může mimo jiné dojít k fatálnímu narušení životních podmínek hmyzu.
Je-li hraničící vzduchová vrstva nasycena plyny kapaliny, pak může pronikání dalších par z vnějšku výrazně ovlivnit povrchové napětí.
Povrchové napětí je silně závislé na teplotě a všeobecně platí, že klesá s rostoucí teplotou. Od kritického bodu je rovno nule.
 8
8Kapilární elevace a deprese
V kapičce kapaliny, například v malé kapce vody nebo plynové bublině uvnitř kapaliny, působí kvůli povrchovému napětí na rozhraní kapalina/plyn zvýšený tlak, taktéž i ve vnitřku mýdlové bubliny. Zvýšení tlaku popisuje Young-Laplaceova rovnice:
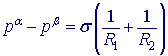
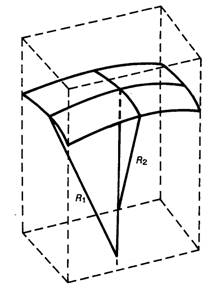
Podmínka mechanické rovnováhy na zakřiveném fázovém rozhraní: rozdíl tlaků na konkávní (pβ) a konvexní (pα) straně rozhraní (obr. 1) je funkcí zakřivení fázového rozhraní (R1, R2 jsou hlavní poloměry křivosti) a mezifázového napětí σ:
Pro kulovité rozhraní (R1 = R2) má Laplaceova-Youngova rovnice tvar:
![]()
Pro rozhraní ve tvaru válcové plochy (R1 = r, R2 = ∞) platí
![]()
 9
9V důsledku zakřivení povrchu kapaliny v kapiláře (úzkou trubici o malém vnitřním poloměru r) vznikne výraznější rozdíl tlaků na konkávní a konvexní straně rozhraní. Při vypuklém (konvexním) tvaru (např. skleněná kapilára se rtutí) bude sloupec stlačován, při vydutém (konkávním) tvaru menisku (případ skleněné smáčivé kapiláry a vody) bude sloupec stoupat nad úroveň volné hladiny.
Tlak pod meniskem v kapiláře je tedy snížen o hodnotu 2σ/r proti tlaku, který působí na volnou hladinu vody. Voda proudí z místa vyššího tlaku (z volné hladiny) do místa nižšího tlaku (k menisku v kapiláře) tak dlouho, až hydrostatický tlak sloupce vody vyrovná kapilární tlak p. Rovnováha kapaliny v tíhovém poli nastane tehdy, bude-li mít kapalina v každé vodorovné rovině stejný tlak. Kapalina s konkávním meniskem tedy musí v kapiláře vystoupit výše vzhledem k okolnímu povrchu, mluvíme o kapilární elevaci, a naopak kapalina s konvexním meniskem poklesne níže, tzv. kapilární deprese. Při rovnováze bude rozdílu tlaku z důvodu zakřivení rozhraní roven hydrostatickému tlaku odpovídajícímu výšce sloupce.
![]()
![]()
kde h je výška kam vystoupí (případně hloubka kam sestoupí) hladina kapaliny v kapiláře a r je poloměr ideálně smáčející nebo ideálně nesmáčející kapaliny.
U celulózních stěn xylému je povrch stěn kapiláry dokonale smáčivý a poloměr křivosti menisku r se rovná poloměru kapiláry. Nesmáčivost pro vodu umožňují karboxylové skupiny celulózy buněčných stěn cév. Po dosazení za povrchové napětí vody při teplotě 20 °C (0,07275 J m-2), za hustotu vody při téže teplotě (998,2 kg m-3) a za tíhové zrychlení (9,807 m s-2) dostaneme:
![]()
![]()
Průměr cévy v xylému bývá 50 až 100 μm. Zjistíme, že voda v takových cévách vystoupá jen do výše 15 až 30 cm nad hladinu vody (tj. nad „vodní rezervoár “). To je příliš málo i pro vyšší byliny, natož pro stromy. Je ale potřeba vzít v úvahu dvě skutečnosti:
1. Cévy jsou zakončeny a obklopeny celulózními stěnami s interfibrilárními mikrokapilárami o průměru 10-7 až 10-8 m. Výpočet podle vzorce pro kapilární elevaci ukazuje, že menisky vody v kapilárách o takovém průměru mohou udržet i vodní sloupce podstatně vyšší, než jsou nejvyšší stromy (sloupce by mohly být až několik tisíc metrů vysoké). Je možné ukázat na modelu trubice o velkém průměru rozvětvené na konci do mikrokapilár, že je-li systém zcela "zavodněn“, budou mikrokapiláry schopny udržet vodu proti zemské tíži i při silném výparu.
2. Voda nestoupá systémem prázdných xylémových cév do korun stromů, ale sloupce vody „rostou“ (prodlužují se) s tím, jak strom roste. Jakmile je kontinuum vody v cévě přerušeno, je postižená kapilára (céva) vyřazena. Voda vystoupí v kapiláře tak vysoko jen tehdy, pokud se sloupec vody v kapiláře nepřetrhne.
 10
10
Zdroje obrázků:
[1,2] http://cs.wikipedia.org/wiki/Adheze
[3,4] http://cs.wikipedia.org/wiki/Povrchové_napětí
[5,6,7] upload.wikimedia.org
[8]
[9]
[10] www.kaheel7.com/eng/ index.php/nature-a-life/