Untitled Document

Na pohybující se těleso působí kromě statických sil také síly dynamické, které při ukončení pohybu opět zanikají. Jedná se o síly odporové či třecí.

1. Tahová odporová síla
Tlakový odpor vzniká při odtržení proudu od tělesa, které obtéká, a vzniku vířivé oblasti. U desky je největší pokud je postavena kolmo ke směru proudění. Nejmenší naopak pokud je postavena rovnoběžně se směrem proudění. Závisí na povaze proudění. V případě laminárního proudění je odporová síla přímo úměrná rychlosti. V případě koule o poloměru ji můžeme vyjádřit jako Stokesovu sílu FS :

V případě turbulentního proudění je síla úměrná druhé mocnině rychlosti, a lze ji vyjádřit vztahem:

Koeficient CD je funkcí Reynosldsova čísla. Při přechodu do turbulentního proudění dochází ke vzniku vírů za pohybujícím se tělesem. Víry se tvoří s
tzv. Strouhalovou frekvencí

kde St je Strouhalovo číslo je funkcí hodnoty CD a nabývá hodnoty mezi 0,12 a 0,23.

Přechod laminárního proudění v turbulentní závisí na hodnotě Reynoldsova čísla:

v je kinematická viskozita, η je dynamická viskozita:. Pokud je hodnota menší než 100 je proudění laminární, pokud je hodnota větší než 100, je proudění turbulentní. Pro Reynoldsovo číslo lze Strouhalovo číslo vyjádřit vztahem:

2. Třecí síla
S narůstající kolmou vzdáleností od desky roste rychlost až na hodnotu nenarušeného proudu. Rychlost se mění zejména v úzké mezní vrsvě kolem desky.

kde S je povrch, u rychlost, ρ hustota. Koeficient třecí síly CT závisí na povrchové struktuře hraniční vrstvy. Například v případě ryb závisí na povrchu kůže jejich těla (např. struktuře šupin apod.)

Pokud bychom zvolili koeficient společný pro tlakovou i třecí odporovou sílu CST, má tento parametr minimální hodnotu jestliže poměr šířky a délky se nachází v rozmezí 0,1 a 0,4.

Na jaký tvar těla v proudící kapalině působí minimální celková odporová síla?

Na plovoucí organizmy působí odporová a třecí síla

K plavání musí živočichové vyvinout mechanický výkon

Živočichové zřídkakdy minou příležitost minimalizovat svoje energetické výdaje, proto i v plavání se snaží uzpůsobit svůj tvar, tak aby při pohybu ve vodě na ně působila co nejmenší odporová síla. Ryby mají často poměr průměru těla k její délce právě: .

Pro pomalé plavce, u kterých je odporová síla lineární funkcí rychlosti, je vhodnější tvar s nejmenším bočním povrchem na nějž působí třecí síla (závislá na druhé mocnině rychlosti). Výhodný je proto kulovitý tvar. Tomu odpovídá poměr X =1, Příčný průřez na kterém závisí tahová síla je roven a povrch je roven:.

Nejmenší odporovou sílu můžeme odhadnout analyticky jako minimum součtu 2 odporových sil působící obecně na válcové těleso v proudící kapalině (derivovat podle poměru X).

pro objekt s příčným průřezem . Pro CD v tomto případě platí, že je rovno přibližně 0,03. Následně vyjádříme sílu v závislosti na 3 veličinách: poměru průměru a délky, objemu V a rychlosti U. Ze vztahu a X = D / L můžeme vyjádřit veličiny D a L:

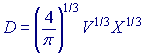
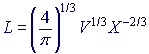
Konstanta C1 zahrnuje odporový koeficient a hustotu vody :

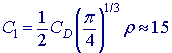
Vztah pro tlakovou sílu ukazuje, že tato síla u ponořeného tělesa roste s poměrem rozměrů. Čím větší poměr průměru k délce, tím větší odpor.

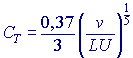
Odporová síla klesá s rostoucím poměrem průměru ku délce s . Celková odporová síla: ja

Pokud za objem dosadíme V=M/ρ a derivací podle X určíme minimum síly FTS , dostáváme závislost geometrického poměru na hmotnosti, danou vztahem:

Rychlost vodních organizmů roste kontinuálně s jejich hmotností. V průměru větší ryby plavou rychleji než menší. Z empirických data vyplývá vztah:. Po dosazení do vztahu pro geometrický poměr dostáváme:

Na základě tohoto modelu tedy vyplývá, že geometrický poměr průměru a délky klesá s rostoucí hmotností. Tedy větší rychlejší organizmy jsou hubenější než menší a pomalejší.

3. Vlnová odporová síla (ventilation drag, wave drag)
Na organizmy, kteří plavou na hladině, působí kromě předchozích sil také tzv. vlnová odporová síla. Pohyb tělesa (živočicha) vytváří rozdílný tlak kolem sebe. Pokud použijeme pojmy příď a záď spojené s pohybem lodi, můžeme tuto odporovou sílu vysvětlit následovně. Před přídí se hromadí voda (tzv. příďová vlna), naopak méně vody je na „zádi“. Tím vzniká rozdíl tlaků na přídi a zádi. Vlnová hloubka h (tj pokles hladiny za pohybujícím se tělesem) je úměrná druhé mocnině rychlosti.
Vlnová odporová síla závisí na exponovaném příčném průřezu tj. ploše Aex . Tato plocha je úměrná šířce w a vlnové hloubce h:

Vlnová síla roste se 4 mocninou rychlosti. Organizmy mohou snížit nebo eliminovat tuto odporovou sílu pokud plavou úplně ponořená. Přesto pokud plavou blízko hladiny, uplatňuje se částečně vlnový odpor. Tato síla je spojena se zrychlením určitého objemu kapaliny mezi tělem a povrchem. Snížení vlnového odporu snížením exponovaného průřezu správnou pozicí při plavání (viz následující obrázek)

4. Dynamická vztlaková síla (lift force)
Nesouměrný profil nosné plochy způsobuje, že vzduch obtéká její horní stěnu věší rychlostí než stěnu spodní. Podle Bernoulliho rovnice je tedy tlak na horní stěnu nosné plochy menší než na spodní stěnu. Na nosnou plochu letadla působí tedy aerodynamická vztlaková síla, která působí proti tíhové síle. Na příčný průřez letadla působí odporová síla, kterou překonává tažná síla motorů.

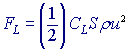
kde amplituda FLo je na stejné úrovni jako odporová síla FD, působící na cylindrický tvar. Frekvence tohoto pohybu je Strouhalova frekvence, závisející na Strouhalově čísle.