Vnitřní a jiné síly

Statické síly

Chůze

V průběhu evoluce se vyvinulo jen velmi málo způsobů pozemního pohybu suchozemských živočichů. Z nich nejefektivnější je bezesporu chůze a běh, pohyb využívající opory končetin.

Chůze se liší od běhu tím, že v každém okamžiku je alespoň jedna noha ve styku s podložkou.
Předpokládejme, že na začátku kroku je pravá noha vzadu a levá vpředu. Krok začíná tak, že se pravá noha odrazí od země a mírně ohnutá překmitne dopředu. Tělo přitom vykoná oblouk na napjaté levé noze. Tím se pravá noha dostane dopředu a levá dozadu.
Tento pohyb se opakuje střídavě s pravou a levou nohou. V dalším textu budeme periodou chůze rozumět dobu trvání dvou po sobě následujících kroků.

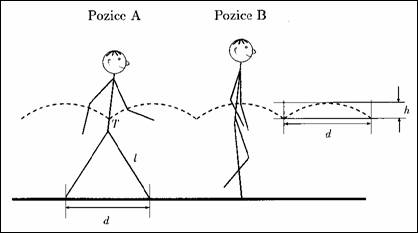
Rozhodující pro odhad mechanické práce konané při chůzi je pohyb těžiště těla, jehož trajektorie je schematicky znázorněna na obr. 1. Těžiště se pohybuje přibližně po křivce složené z částí oblouků a energie nutná k udržení tohoto pohybu je dána prací potřebnou ke zvýšení polohy těžiště o převýšení h. V každém kroku tedy musíme tedy dodat energii E = m.g.h, kterou při následném poklesu těžiště těla již nezískáme zpět. Z jednoduché geometrie (viz obr. 2) přímo plyne:

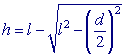
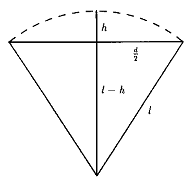
kde význam symbolů je zřejmý z obrázku. Dosadíme-li typické hodnoty l = 0,95 m, d = 0,8 m, dostaneme h = 0,1 m, což je asi desetina délky kroku.

Tzv. biomechanická zásada uvádí, že při chůzi po vodorovné rovině musíme vykonat asi 1/15 mechanické práce, nutné pro zvednutí těla ve svislém směru o tutéž vzdálenost. Náš jednoduchý odhad poskytl poněkud vyšší hodnotu. Ve skutečnosti je totiž pohyb těžiště komplikovanější, než naznačuje obr. 1, a veličina h je skutečně menší. Při chůzi se koordinovaně pohybuje celé tělo, což efektivně vyhlazuje trajektorii těžiště a navíc rozkládá mechanický výkon na více svalových skupin. K tomu přispívá především:

1) Ohýbání chodidla v kotníku. Odrážíme se špičkou nohy, což prodlužuje efektivní délku nohy v závěrečné fázi kroku, a tím krok prodlužuje.

2) Natáčení pánve. Pánev natáčíme vždy vzhůru na straně opěrné nohy, natočení je maximální v pozici B z obr. 1. Tímto snížíme maximální výšku těžiště těla, a tak zmenšíme hodnotu převýšení h. Při závodní chůzi značné vytáčení pánve minimalizuje zvlnění trajektorie těžiště a s ním související výdej energie.

3) Pohyb horních končetin. Vykročení doprovázené pohybem rukou posouvá těžiště těla vzhůru vzhledem k trupu. Takto v pozici A zvýšíme minimální výšku těžiště a opět zmenšíme h.

S využitím biomechanické zásady je již jednoduché odhadnout průměrný výkon při chůzi jako 1/15 výkonu nutného ke svislému stoupání rychlostí chůze. Tedy: Pokud počítáme s rychlostí chůze u = 4 km/h (1,1 m/s), dostaneme výkon přibližně 60W.

Zajímavé je porovnat chůzi se sprintem na 100 m. Při desetkrát pomalejší chůzi vydáváme dvacetkrát nižší výkon. Chůze je tedy přibližně dvakrát efektivnější než rychlý běh.

Vertikální pohyb těžiště, a tedy i očí, si běžně při chůzi ani neuvědomíme. Zřetelný se stane, např. půjdeme-li vedle jiného chodce tak, že mezi našimi kroky bude fázový posuv π / 2.

Rychlost chůze

Z pohledu mechaniky je překmitnutí nohy vpřed kyvem fyzického kyvadla otočně upevněného v kyčelním kloubu. Chůze bude nejpohodlnější a nejméně únavná, pokud frekvence kroků bude blízká frekvenci vlastních kmitů nohy. Pro odhad této frekvence předpokládejme, že kyv nohy je harmonický pohyb, pro jehož periodu platí:

,

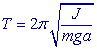kde:     J - moment setrvačnosti nohy vzhledem k ose otáčení
            a - vzdálenost těžiště nohy od osy otáčení.

Moment setrvačnosti nohy a polohu těžiště vzhledem k ose otáčení můžeme odhadnout jen přibližně. Pro výpočet momentu setrvačnosti předpokládejme, že noha je homogenní tyč. Její zúžení v dolní části je alespoň částečně kompenzováno chodid-lem, které tvoří dodatečný přívažek ve velké vzdálenosti od osy otáčení. Těžiště nohy je přibližně ve 40 % procentech její délky tj. a = 0,4.l. Za těchto předpokladů pro periodu vlastních (netlumených) kmitů dostaneme:

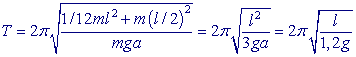
K výpočtu momentu setrvačnosti J jsme použili Steinerovu větu. Při průměrné délce kroku 0,8 m by byla rychlost chůze 3,2 km/h, což je hodnota blízká skutečné rychlosti pomalé a pohodlné chůze. Chceme-li chůzi zrychlit, musíme silou svých svalů urychlit překmitnutí nohy, což vyžaduje úsilí, které je neúměrné přírůstku rychlosti. Zdvojnásobení rychlosti chůze vyžaduje více než dvojnásobný svalový výkon.

Závislost rychlosti chůze na velikosti člověka

Srovnáme-li rychlost chůze dospělého člověka a malého dítěte, zjistíme reálný fakt, že  malé dítě jde pomaleji. Pokusme se odhadnout, jak závisí rychlost chůze na charakteristické délce člověka. Pro rychlost chůze platí:

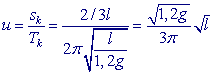
kde sk je délka 1 kroku, kterou můžeme odhadnout jako 2/3 délky nohy.Rychlost je tedy úměrná odmocnině délky nohy. Čtyřikrát vyšší člověk má dvakrát větší rychlost. Co se týče frekvence:

Kroková frekvence se zvětšuje se zmenšující se velikostí, čtyřikrát vyšší člověk má dvakrát menší krokovou frekvenci.

Proč při chůzi máváme rukama?

Mávání rukama, jak již bylo zmíněno dříve, zvyšuje polohu těžiště v okamžiku maximálního vykročení, a tak snižuje skutečnou hodnotu převýšení h. Obě horní končetiny tvoří asi 10 % hmotnosti těla a jejich vychýlením o 30°C dosáhneme zvýšení těžiště přibližně o 5 % dříve spočtené hodnoty h. I pohyb rukou vyžaduje práci svalů, při mávání rukama však zapojujeme do činnosti jiné svalové skupiny, a tak pomáháme odlehčit svalům nohou.

Malé vyhlazení trajektorie těžiště není jediným důvodem pohybu rukou. Mávání rukama a případně i natáčení horní části trupu kompenzuje moment hybnosti nohou vzhledem ke svislé ose těla. S kmitavým pohybem nohou při chůzi souvisí oscilující moment hybnosti, který, pokud by tělo bylo izolovanou soustavou, by musel být kompenzován rotačním pohybem celého trupu případně pohybem rukou v protifázi s pohybem nohou. Naše tělo samozřejmě není při chůzi izolovanou soustavou, a tak můžeme kráčet zcela strnule bez jakéhokoliv rotačního pohybu trupu či rukou. Trup je pak udržován v klidu třecí silou mezi chodidly a podložkou a s ní spojeným momentem síly. Moment třecí síly však torzně namáhá naše dolní končetiny a činí takovouto chůzi velmi nepohodlnou.

Mechanická práce a únava

Lidské tělo, stejně jako těla jiných živočichů, je složitým systémem a nelze proto na něj beze zbytku aplikovat výsledky jednoduchých mechanických úvah. Jen dva příklady pro ilustraci:

a) Napjatá pružina nekoná práci, ale napjatý sval se unaví. Aby se konala mechanická práce, je nutný posun tělesa za současného působení síly. Napjatá a fixovaná pružina nekoná žádnou mechanickou práci, ale pouhé stání člověka na místě je únavné. Z hlediska výdeje mechanické energie je lhostejné, zda stojíme na napjatých nohách, nebo v podřepu. Je však výhodnější využívat pevné opory kostry než držet tíhovou sílu těla napjatými svaly. Chůze z kopce unavuje, i když těžiště těla trvale klesá.

b) Sval pracuje hospodárněji, podává-li menší výkon. Při malém výkonu probíhá ve svalu současně i regenerace svalové hmoty, takže člověk je schopen vykonat více práce nízkým výkonem za dlouhou dobu než velkým úsilím koncentrovaným do krátkého času. Například při dlouhém stoupání je výhodnější pomalé vytrvalé tempo než rychlý výstup s častými přestávkami

Zdroje:
Zdeněk Bochníček, Školská fyzika 4/1995-1996
Štaigler, M., Červinka, L.: Aplikace technické mechaniky pro učitele, SPN, Praha 1971