|
Světelné paprsky se nešíří atmosférou přímočaře, ale po zakřivených drahách v důsledku toho, že se index lomu vzduchu mění s výškou. U plynů je totiž index lomu n závislý na hustotě r podle vztahu (1.5.7). Hustoty vzduchu s rostoucí výškou ubývá, a tudíž i index lomu vzduchu s výškou klesá.
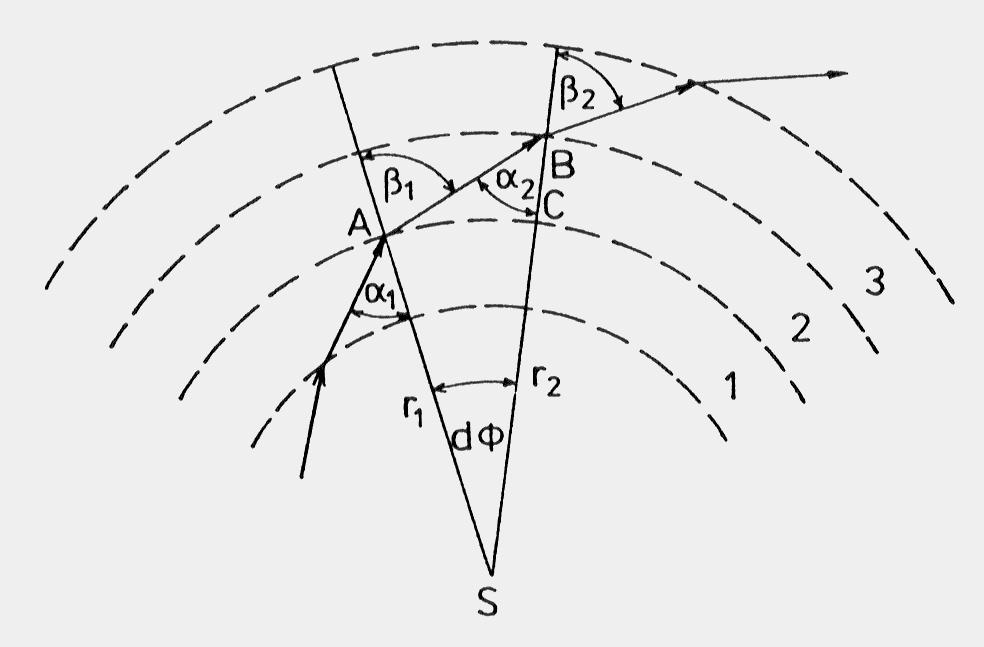
Abychom mohli popsat trajektorii světelných paprsků, vycházíme ze zjednodušené představy: Atmosféru si představíme složenou z infinitezimálně tenkých sférických vrstev. Tři z těchto vrstev vidíme schematicky zakresleny na obr. 1.5.2 jako prostředí 1,2,3 jejichž rozhraní znázorňují čárkované části kružnic o středu v bodě S (středu Země). Předpokládáme, že každá z těchto vrstev je charakterizována určitou hustotou, a tudíž i indexem lomu, které se na rozhraní skokem mění. Zakreslený paprsek se tedy nejeví jako plynulá křivka, ale představuje lomenou čáru se zlomy na jednotlivých fiktivních rozhraních.
Paprsek ve vrstvě 1 dopadá na rozhraní s vrstvou 2 pod úhlem dopadu a1, láme se do této vrstvy pod úhlem b1, dopadá na rozhraní s vrstvou 3 pod úhlem a2, láme se do ní pod úhlem b2, atd... .
Jsou - li indexy lomu ve vrstvách 1,2,3 po řadě n1, n2, n3, platí podle Snellova zákona lomu (1.5.2)
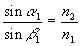atd. (1.5.10)
Jsou- li |AS|=r1 a |BS|=r2 vzdálenosti bodů A a B od středu Země, pak z trojúhelníka ABS vyplývá podle sinové věty a z platnosti trigonometrického vzorce sin(p-b1)=sin b1
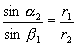, (1.5.11)
Dosadíme - li za sinb1 do (1.5.10), získáme vztah
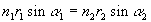, (1.5.12)
Protože uvažované infinitezimální vrstvy můžeme volit zcela libovolně, platí (1.5.12) pro jakékoliv rozhraní v atmosféře rovnoběžné s ideálním tvarem povrchu zemského tělesa. Obecně tedy platí pro trajektorii daného paprsku
n.r.sina=C , (1.5.13)
kde n značí index lomu vzduchu v určitém bodě, r vzdálenost tohoto bodu od středu Země, a úhel sevřený paprskem a vertikálně orientovanou přímkou a C je pro daný paprsek konstanta určená počátečními podmínkami.
Rovnici (1.5.13) můžeme použít k vyjádření křivosti trajektorie světelného paprsku. K tomuto
účelu si označíme symbolem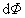 
infinitezimální úhel sevřený polopřímkami SA a SB, dále zaveďme dr=r2–r1. Logaritmickým diferencováním rovnice (1.5.13)odpovídajícím elementu trajektorie paprsku od bodu A do bodu B dostáváme
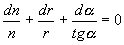. (1.5.14)
Protože vrstvu 2 lze volit zcela libovolně, upustíme u veličin a a r od psaní indexů.
Pro nekonečně malý úhlový element můžeme oblouk AC aproximovat úsečkou a v pravoúhlém trojúhelníku ABC pak platí
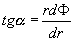, (1.5.15)
dosadíme-li za dr/r do vztahu (1.5.14),obdržíme
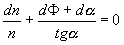. (1.5.16)
Z jednoduché geometrické úvahy vyplývá, že celkový úhel stočení paprsku dj v uvažované infinitezimální vrstvě atmosféry (vrstva 2 na obr.1.5.2) je roven
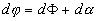, (1.5.17)
Definujeme křivost K trajektorie světelného paprsku
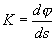, (1.5.18)
kde ds je délka dráhy uražená paprskem v myšlené infinitezimální vrstvě.
Z obrázku obr.1.5.2 je zřejmé, že
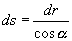. (1.5.19)
Křivost K tedy představuje úhel stočení trajektorie, urazí-li paprsek v atmosféře dráhu o jednotkové délce.
Vyjádříme-li stočení paprsku v obloukové míře, potom převrácená hodnota křivosti 1/K udává v daném bodě trajektorie poloměr kružnice, pomocí níž lze v nejbližším (nekonečně malém) okolí uvažovaného bodu aproximovat zmíněnou trajektorii.
Dosadíme-li vztahy (1.5.17) a (1.5.19) do (1.5.18), dostáváme
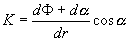
a s použitím vztahu (1.5.16) dostaneme
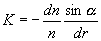. (1.5.20)
V našem případě se můžeme bez podstatnější újmy na přesnosti spokojit s představou, že Země je dokonalá koule o poloměru rz a že tedy vzdálenost r uvažovaného bodu v atmosféře od středu Země je roven součtu konstantního poloměru země rz a výšky z nad zemským povrchem, tj.
dr=d(rz+z)=dz,(1.5.21)
neboť drz=0. Vztah (1.5.20) pak lze upravit do výsledného tvaru
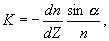(1.5.22)
když dn/dz, interpretujeme v daném bodě jako derivaci indexu lomu vzduchu podle vertikální souřadnice a K představuje v tomto bodě křivost trajektorie takového paprsku, jenž zde svírá s vertikálou úhel a.
Zpracováno na základě literatury [1].
Zpět