 |
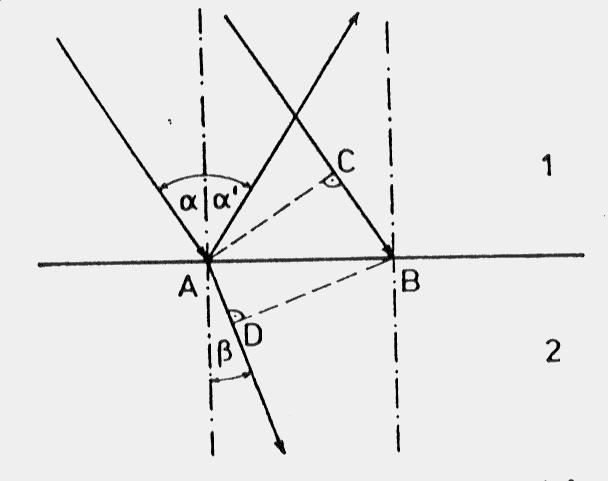
Uvažujeme dvě elektricky nevodivá prostředí, vzájemně oddělená nepohyblivým rovinným rozhraním (viz obr. 1.5.1). Prvé z nich, označené 1, je charakterizováno relativní permitivitou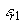 a relativní magnetickou permeabilitou
a relativní magnetickou permeabilitou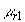 , zatímco druhé se vyznačuje relativní permitivitou
, zatímco druhé se vyznačuje relativní permitivitou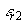 a relativní magnetickou permeabilitou
a relativní magnetickou permeabilitou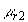 . Definujeme veličinu n21 relativní index lomu prostředí 2 vzhledem k prostředí 1 jako podíl rychlostí šíření světelných paprsků v1 (v prostředí 1) ku rychlosti v2(v prostředí 2). Podle (1.4.1) platí
. Definujeme veličinu n21 relativní index lomu prostředí 2 vzhledem k prostředí 1 jako podíl rychlostí šíření světelných paprsků v1 (v prostředí 1) ku rychlosti v2(v prostředí 2). Podle (1.4.1) platí
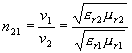 , (1.5.1)
, (1.5.1)
Na obr.1.5.1 máme znázorněn světelný paprsek, který v bodě A dopadá z prostředí 1 na zmíněné rozhraní pod úhlem a, částečně je odrážen zpět do prostředí 1 po úhlem a' a částečně se lomí do prostředí 2 pod úhlem b. Kromě právě zmíněného paprsku si povšimněme paprsku s ním rovnoběžného, jenž v bodě B dopadá na dané rozhraní a jako bod C označme průsečík tohoto druhého paprsku s rovinou k němu kolmou a procházející bodem A. Podobně označme D průsečík lomeného paprsku s rovinou k němu kolmou a obsahující bod B. Prvá ze zmíněných rovin vyznačených na obr.1.5.1 přerušovanými čarami představuje vlnoplochu příslušející elektromagnetickému vlnění vytvářejícímu svazek rovnoběžných paprsků dopadajících na uvažované rozhraní v okamžiku, kdy prvý z vyznačených dvou paprsků dosáhne bodu A. Druhá odpovídá vlnoploše příslušející lomeným paprskům v okamžiku, kdy druhý paprsek se právě částečně odráží a lomí v bodě B. Z triviálních vlastností vlnoploch je okamžitě zřejmé, že čas potřebný na to, aby světelný paprsek urazil v prostředí 1 dráhový úsek CB, musí být roven času t, za který lomený paprsek proběhne v prostředí 2 dráhu délky AD. To však znamená |AD|=v2t a |CB|=v1t. Dosadíme-li odtud do (1.5.1), dostáváme
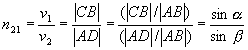 , (1.5.2)
, (1.5.2)
(n21někdy označujeme nr), což vyjadřuje základní zákon lomu světelných (elektromagnetických) paprsků, jenž se označuje jako Snellův zákon.
Spolu s lomem (refrakcí ) světelných paprsků dochází k jejich částečnému odrazu (reflexi) na uvažovaném rozhraní, který se řídí následujícími dvěma dílčími zákony:
1. Odražený paprsek zůstává v rovině dopadu určené dopadajícím paprskem a kolmicí k uvažovanému rozhraní v bodě dopadu daného paprsku. Stejný zákon platí i pro paprsek lomený do druhého prostředí.
2. Úhel odrazu se rovná úhlu dopadu, tj. na obr.1.5.1 a= –a' (měříme vždy od paprsku ke kolmici na dané rovinné rozhraní).
V případě v1>v2 se paprsek lomí z prostředí opticky řidšího do prostředí opticky hustšího a podle (1.5.2) musí platit a>b ( lom ke kolmici ), což je zřejmé z obr.1.5.1. V opačném případě v1<v2 se jedná o lom od kolmice a<b a paprsek se šíří z prostředí opticky hustšího do prostředí opticky řidšího. Ve druhém z právě uvedených dvou případů existuje mezní úhel dopadu aM, při němž lomený paprsek směřuje rovnoběžně s rovinným rozhraním a za situace, kdy úhel dopadu b>aM, dochází k totálnímu odrazu, při němž žádný lom do opticky řidšího prostředí nevzniká. Hodnota závisí na relativním indexu lomu daných dvou prostředí a určíme ji z (1.5.1), dosadíme-li za b pravý úhel.
Jestliže jako prvé prostředí uvažujeme vakuum, potom v (1.4.1) dosadíme er1=mr1=1 a v1=c ,tzn.
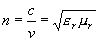 , (1.5.3)
, (1.5.3)
kde v značí rychlost šíření světelných ( obecně elektromagnetických ) paprsků v daném prostředí o relativní permitivitě er a relativní magnetické permeabilitě mr. Veličina n se pak nazývá absolutní index lomu tohoto prostředí (v našich dalších úvahách ji budeme pro krátkost označovat pouze index lomu).
Máme-li dvě prostředí o absolutních indexech lomu n1 a n2, potom pro relativní index lomu druhého prostředí vůči prvnímu platí
| l (nm) | n |
|---|---|
| 400 | 1,0002983 |
| 500 | 1,0002943 |
| 600 | 1,0002931 |
| 700 | 1,0002910 |
| (800 | 1,0002902) |
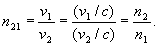 , (1.5.4)
, (1.5.4)
Absolutní index lomu vzduchu se obvykle poněkud zvětšuje s klesající vlnovou délkou elektromagnetického záření, což názorně ukazuje tab. 1.5.1 a v oblasti viditelného záření (světla) dále platí se značnou přesností, že hodnota n-1 je pro danou vlnovou délku úměrná hustotě vzduchu r, tzn.
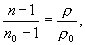 (1.5.5)
(1.5.5)
kde n0, resp. n značí absolutní index lomu vzduchu o hustotě r0, resp. r. Upravíme-li vztah (1.5.5) pomocí stavové rovnice
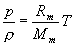 , (1.5.6)
, (1.5.6)
v níž p je tlak, hustota vzduchu, Rm jeho molární plynová konstanta, Mm molární hmotnost a T teplota v kelvinech. Podíl Rm/Mm je měrná plynová konstanta vzduchu r= 287 J.kg-1.K-1 (viz [16]). Odtud okamžitě dostaneme
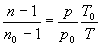 , (1.5.7)
, (1.5.7)
Hodnoty p0, T0, při nichž má vzduch absolutní index lomu n0, považujeme za konstantní při povrchu Země, zatímco p, T budeme uvažovat jako funkce výšky nad zemským povrchem. Derivováním (1.5.7) podle vertikální souřadnice z a užitím rovnice hydrostatické rovnováhy
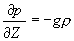 , (1.5.8)
, (1.5.8)
kde g je velikost tíhového zrychlení, potom získáme
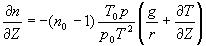 . (1.5.9)
. (1.5.9)
Derivace 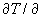 z představuje lokální změnu teploty připadající na jednotkovou vzdálenost ve vertikálním směru a dosazením číselných hodnot velikosti tíhového zrychlení a měrné plynové konstanty vzduchu posléze získáme g/r=0,0342 K.m-1. Dosazením za p z (1.5.6) do (1.5.8) lze ukázat, že poměr g/r představuje absolutní hodnotu lokálního poklesu teploty připadajícího na jednotkovou vzdálenost ve vertikálním směru v tzv. homogenní atmosféře, tj. za situace, kdy hustota vzduchu je konstantní s výškou. Z (1.5.9) tedy vyplývá, že v případě, kdy teplota vzduchu klesá s výškou pomaleji než o 3,42 K na 100m popř. se s výškou nemění (izotermie) nebo dokonce roste (teplotní inverze), tj.
z představuje lokální změnu teploty připadající na jednotkovou vzdálenost ve vertikálním směru a dosazením číselných hodnot velikosti tíhového zrychlení a měrné plynové konstanty vzduchu posléze získáme g/r=0,0342 K.m-1. Dosazením za p z (1.5.6) do (1.5.8) lze ukázat, že poměr g/r představuje absolutní hodnotu lokálního poklesu teploty připadajícího na jednotkovou vzdálenost ve vertikálním směru v tzv. homogenní atmosféře, tj. za situace, kdy hustota vzduchu je konstantní s výškou. Z (1.5.9) tedy vyplývá, že v případě, kdy teplota vzduchu klesá s výškou pomaleji než o 3,42 K na 100m popř. se s výškou nemění (izotermie) nebo dokonce roste (teplotní inverze), tj. 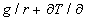 z>0, platí
z>0, platí 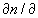 z<0, to znamená, že absolutní index lomu klesá s výškou. Za anomálních situací velice rychlého poklesu teploty vzduchu s výškou (více než o 3,42 K na 100 m) dochází naopak k inverzi hustoty vzduchu (vzrůstu hustoty s výškou) a ke zvětšování absolutního indexu lomu s vertikální souřadnicí. V prvém případě paprsek šířící se atmosférou šikmo vzhůru postupuje do opticky stále řidšího prostředí a v důsledku lomu se zakřivuje od kolmice, tj. ve smyslu odpovídajícím zakřivení zemského povrchu, zatímco ve druhém, v podstatě anomálním případě vyskytujícím se někdy v silně přehřáté přízemní vrstvě vzduchu (viz dále), vzniká zakřivení obdobně postupujícího paprsku ke kolmici, tj. ve smyslu opačném k zakřivení zemského povrchu.
z<0, to znamená, že absolutní index lomu klesá s výškou. Za anomálních situací velice rychlého poklesu teploty vzduchu s výškou (více než o 3,42 K na 100 m) dochází naopak k inverzi hustoty vzduchu (vzrůstu hustoty s výškou) a ke zvětšování absolutního indexu lomu s vertikální souřadnicí. V prvém případě paprsek šířící se atmosférou šikmo vzhůru postupuje do opticky stále řidšího prostředí a v důsledku lomu se zakřivuje od kolmice, tj. ve smyslu odpovídajícím zakřivení zemského povrchu, zatímco ve druhém, v podstatě anomálním případě vyskytujícím se někdy v silně přehřáté přízemní vrstvě vzduchu (viz dále), vzniká zakřivení obdobně postupujícího paprsku ke kolmici, tj. ve smyslu opačném k zakřivení zemského povrchu.
Zpracováno na základě literatury [1]
Zpět