V souvislosti s předcházejícími experimenty se fyzikové dostali do nové situace. Nikdy předtím nebyli nuceni k vysvětlení určitého fyzikálního jevu - elektromagnetického záření - použít dva zcela různé přístupy:

• vlnový popis elektromagnetického záření,
• kvantový popis elektromagnetického záření.

Vlnový popis elektromagnetického záření vysvětloval, v souladu s experimentem, mnoho optických jevů, především interferenci a difrakci. Podle tohoto modelu se elektromagnetické záření šíří ve formě vln se spojitě rozloženou energií.

Kvantový popis elektromagnetického záření byl úspěšný při objasnění fotoelektrického jevu a Comptonova jevu. Podle představ tohoto modelu má interakce elektromagnetického záření s hmotou kvantový charakter - záření se při interakci chová jako soubor jednotlivých kvant energie - fotonů s vlastnostmi charakteristickými pro částice.

Kterému popisu máme věřit? Jakým způsobem chápat vlastnosti elektromagnetického záření?

Naše poznání okolního světa postupuje od chápání jednodušších vlastností objektů ke složitějším, od jednoduššího popisu ke složitějšímu. V průběhu vývoje fyzikálního poznání vznikla představa částice jako objektu, jehož pohyb je popsán Newtonovými rovnicemi. Vedle toho vznikla představa pole (např. elektromagnetického pole), které již Newtonovými rovnicemi popsat nelze. Vlastnosti částic jsou v tomto pojetí neslučitelné s vlastnostmi vln: objekt je buď částicí nebo vlnou. Existence vlnových a částicových vlastností elektromagnetického záření zpochybnila představu neslučitelnosti vlastností vln a částic. V dalším vývoji se ukázalo, že elektromagnetické záření i další objekty (viz odstavec 2.5) nemají zcela vyhraněné (krajní) vlastnosti, tj. vykazují vlnové i částicové vlastnosti. Tomuto poznání pak bylo nutné přizpůsobit i fyzikální popis těchto objektů¹³.

Je nutné přijmout představu, že vlnová i částicová povaha je vlastní elektromagnetickému záření. Tentýž paprsek, který se ohýbá difrakcí na štěrbině či mřížce, může způsobit emisi fotoelektronů z vhodného povrchu kovu. Vlnová teorie a kvantová hypotéza proto nejsou rozporné (i když by se tak na první pohled mohlo zdát), ale vzájemně se doplňují při popisu vlastností elektromagnetického záření.

Elektromagnetické záření má vlnové i částicové vlastnosti. Vlnový a kvantový popis se vzájemně doplňují při popisu elektromagnetického záření.

Obr. 4-1: Na dvojštěrbinu dopadá monofrekvenční elektromagnetické záření. Na fotografickém filmu (fotografické desce) vzniká typický interferenční obrazec. Při bližším pohledu na fotografickou desku však zjišťujeme, že vzniklý obrazec se skládá z malých černých teček.

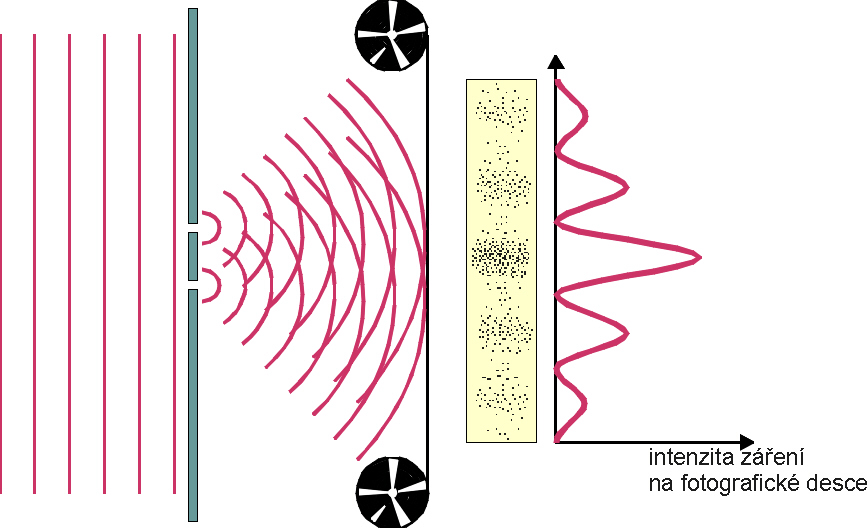
Využijme uvedených poznatků a připomeňme si nejjednodušší interferenční pokus: interferenci monofrekvenčího světla na dvojštěrbině (obr. 4-1). Na fotografické desce vidíme typický interferenční obrazec, který se skládá z tmavších a světlejších proužků. Došlo k interferenci světla v souladu s vlnovou teorií. Při bližším pohledu na fotografickou desku však zjišťujeme, že přechod mezi tmavými a světlými proužky není plynulý. Ve skutečnosti se tmavé oblasti skládají z malých černých teček, jejichž hustota se zmenšuje směrem k světlejším místům. Vysvětlení je následující. Při dopadu elektromagnetického záření na fotografickou desku (interakce záření s fotografickou emulzí) se uplatňují jeho částicové vlastnosti. Každé bodové zčernání vyvolal právě jeden foton, který v daném místě způsobil na citlivé vrstvě fotografické emulze chemickou reakci.

Ukazuje se, že představa o kvantech záření - nositelích nejen energie, ale i hybnosti je nutná k popisu libovolných procesů interakce záření s látkou, a že kvantovanost (diskrétnost) záření je jeho fundamentální vlastností. Tak vznikla představa o elektromagnetickém záření jako o souboru kvant energie - fotonů. Fotony mají některé vlastnosti částic, mají energii, hybnost, jsou vyzařovány a pohlcovány v každém procesu v celku, ale současně jim přísluší i vlnové vlastnosti projevující se například při interferenci světla.

Pokračujme v našem interferenčním pokusu. Snižme intenzitu dopadajícího záření na dvojštěrbinu tak, aby mezi zdrojem a fotografickou deskou bylo množství elektromagnetické energie odpovídající pouze jedinému fotonu - mezi zdrojem a fotografickou deskou je nejvýše jeden foton¹⁴. Při experimentu vzniká naprosto stejný inteferenční obrazec jako předtím (doba osvětlení desky musí být samozřejmě větší). Z toho vyplývá, že foton nemůže mít jen čistě částicové vlastnosti (nemůže být obyčejnou částicí), ale má i vlnovou povahu. Částicové vlastnosti fotonu se projevují bodovým zčernáním. Vlnové vlastnosti způsobují, že dopad mnoha fotonů vytváří interferenční obraz. Každý jednotlivý foton má částicové i vlnové vlastnosti. Vlnově částicový charakter chování fotonů je tedy důvodem vlnově částicových vlastností elektromagnetického záření.

Zkoumáním kvantových vlastností elektromagnetického záření se poprvé setkáváme s vlastnostmi jevů probíhajících v mikrosvětě. Dříve jsme studovali jen jevy, které probíhají ve světě dostupném naší smyslové zkušenosti, světě intuitivně přijatelném, v němž platí zákony klasické fyziky. Je přirozené, že nově objevené jevy (fotoelektrický jev, Comptonův jev) se snažíme popsat pomocí pojmů a představ, které již známe (pojmy částice a vlny). Objekty mikrosvěta jsou však mnohokrát menší než předměty naší každodenní zkušenosti a neexistují důvody, proč by tyto objekty měly být popsatelné jednoduše pomocí pojmů klasické fyziky. Musíme se proto spokojit s konstatováním že:

Foton je objektem mikrosvěta, který má částicové i vlnové vlastnosti, ale není ani částicí ani vlnou.

Foton má některé částicové vlastnosti, ale není přitom částicí. To znamená, že mu nemůžeme připisovat všechny vlastnosti částic, ale je ty z nich, které můžeme experimentálně prokázat. Nemůžeme například hovořit o trajektorii fotonu. Kdybychom to udělali, museli bychom při interferenčním pokusu na dvojštěrbině připustit, že foton prošel jednou nebo druhou štěrbinou¹⁵. Za těchto okolností bychom však již nedokázali vysvětlit vznik interferenčního obrazce. Musíme se tedy vzdát myšlenky, že můžeme pro daný foton určit místo jeho dopadu na stínítku. Je nutné přistoupit k novému způsobu popisu chování fotonu. Podle tohoto přístupu je možné určit pouze pravděpodobnost s jakou foton dopadne do okolí daného místa na fotografické desce. Co však toto tvrzení znamená?

Uveďme si příklad: Víme, že při házení obvyklou hrací kostkou hodíme jedničku s pravděpodobností 1/6 (16,7 procent), sudé číslo padne s pravděpodobností 3/6 = 1/2 (50 procent) a s pravděpodobností 5/6 (83,3 procent) hodím číslo větší než jedna. Provedeme-li nyní sérii 600 hodů a budeme-li si zapisovat výsledky, pak po sečtení jednotlivých úspěšných hodů nám vyjde tabulka:
 

padne:	pravděpodobnost události	počet úspěšných hodů (celkem 600 pokusů) 16
jednička	1/6	100
sudé číslo (2,4,6)	1/2	300
číslo větší než jedna (2,3,4,5,6)	5/6	500

¹⁶Při praktickém provedení pokusu se jednotlivé počty úspěšných hodů mohou nepatrně lišit od hodnot uvedených v tabulce. Podle matematické statistiky je pravděpodobnost události dána vztahem P = m / n (kde n je celkový počet pokusů a m je počet pokusů vyhovujících podmínce pro danou událost) přesně jen pro nekonečný celkový počet pokusů (). Pro konečný celkový počet pokusů n je číslo m / n jen přibližně rovno "ideální" hodnotě P. (S rostoucím počtem pokusů je však tato rovnost splněna stále přesněji.)

Průběh exponování fotografie dává možnost si představit kvantový charakter světla - obraz je složen z jednotlivých bodů. (uvedené fotografije jsou pozitivy - dopadu fotonu na fotografickou desku (negativ) odpovídá na pozitivu světlý bod)

Když řekneme, že při hodu kostkou padne jednička s pravděpodobností 1/6, pak při praktické realizaci většího počtu hodů nám jednička padne v 1/6 z celkového počtu hodů (v našem příkladu 100 krát z 600).

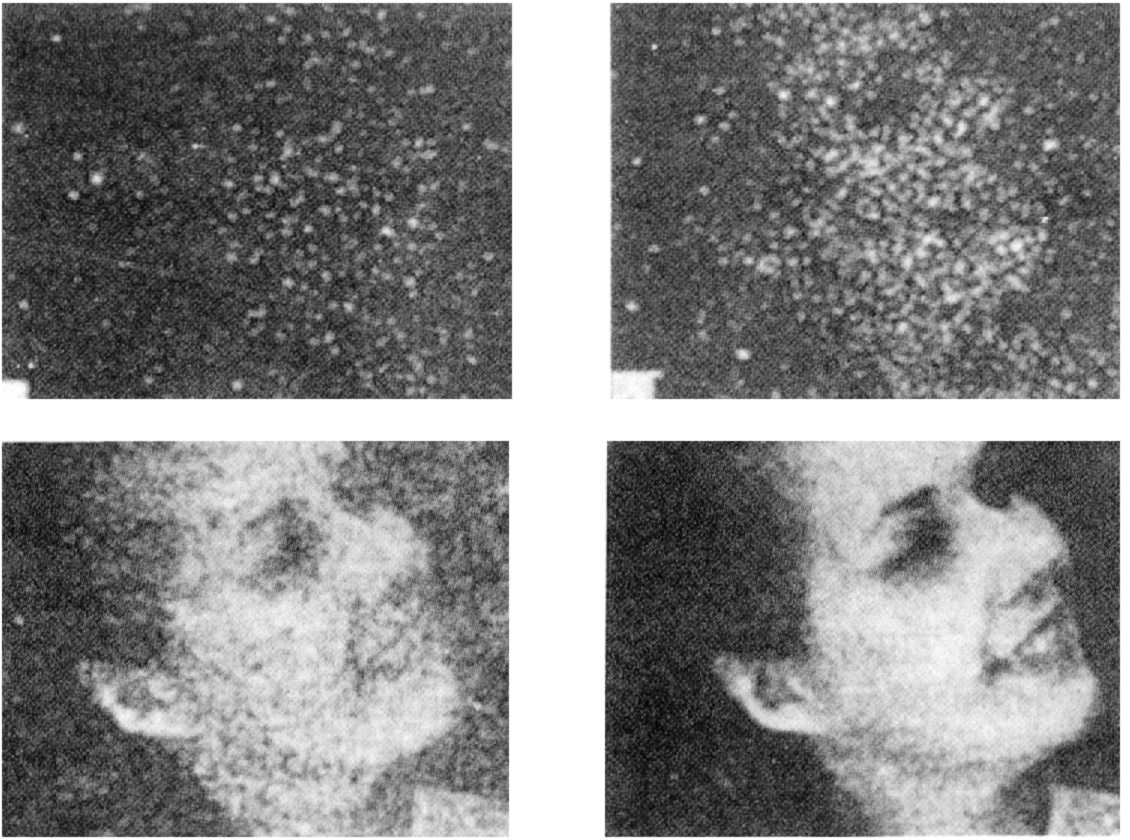
V tomto smyslu musíme rozumět i tvrzení o pravděpodobnosti dopadu fotonu do okolí určitého bodu. Každý jednotlivý foton dopadá na fotografickou desku do zcela náhodného místa (nejsme schopni předpovědět místo dopadu jednotlivého fotonu). Při dopadu většího množství fotonů však do okolí míst s větší pravděpodobností zásahu dopadá větší množství fotonů - v daném místě pozorujeme intenzivnější zčernání fotografické desky.

Míra zčernání fotodesky je úměrná intenzitě záření (vypočítané pomocí vlnové teorie) v daném místě stínítka. Čím větší je intenzita záření v daném místě stínítka, tím více fotonů do něj dopadá, čemuž odpovídá větší míra zčernání fotografické desky (obr. 4-1).

Odtud už lze vyvodit tvrzení:

Pravděpodobnost dopadu fotonu do okolí daného místa je úměrná velikosti intenzity elektromagnetického záření v témže místě.

• Úlohy

1. Stručně popište a porovnejte fotoelektrický jev a Comptonův jev.

 
2. Pokuste se vysvětlit vlastnosti fotonů a důvody vzniku fotonové hypotézy.